Parabolic SAR

Bollinger Band Breakouts

Basically the opposite of "Playing the Bands" and betting on reversion to the mean is playing Bollinger Band breakouts. Breakouts occur after a period of consolidation, when price closes outside of the Bollinger Bands. Other indicators such as support and resistance lines (see: Support & Resistance) can prove beneficial when deciding whether or not to buy or sell in the direction of the breakout.
The chart of Wal-Mart (WMT) below shows two such Bollinger Band breakouts:

Bollinger Band Breakout through Resistance Buy Signal

Price breaks above the upper Bollinger Band after a period of price consolidation. Other confirming indicators are suggested, such as resistance being broken in the chart above of Wal-Mart stock.

Bollinger Band Breakout through Support Sell Signal

Price breaks below the lower Bollinger Band. It is suggested that other confirming indicators be used, such as a support line being broken, such as in the example above of Wal-Mart stock breaking below support.

This strategy is discussed by the man who created Bollinger Bands, John Bollinger, in his book Bollinger on Bollinger Bands Bollinger Bands can also be used to determine the direction and the strength of the trend. The chart below of the E-mini S&P 500 Futures contract shows a strong upward trend:

Bollinger Band Showing a Strong Trend
The chart above of the E-mini S&P 500 shows that during a strong uptrend, prices tend to stay in the upper half of the Bollinger Band, where the 20-period moving average (Bollinger Band centerline) acts as support for the price trend.

The reverse would be true during a downtrend, where prices would be in the lower half of the Bollinger Band and the 20-period moving average would act as downward resistance.

Bollinger Bands adapt to volatility and thus are useful to options traders, specifically volatility traders. The next page describes how to use Bollinger Bands to make better options trades.

Playing the Bollinger Bands

Playing the bands is based on the premise that the vast majority of all closing prices should be between the Bollinger Bands. That stated, then a stock's price going outside the Bollinger Bands, which occurs very rarely,
should not last and should "revert back to the mean", which generally means the 20-period simple moving average. A version of this strategy is discussed in the book
Trade Like a Hedge Fund by James Altucher.
Buy Signal
In the example shown in the chart below of the E-mini S&P 500 Future, a trader buys or buys to cover when the price has fallen below the lower Bollinger Band.

Sell Signal

The sell or buy to cover exit is initiated when the stock, future, or currency price pierces outside the upper Bollinger Band. These buy and sell signals are graphically represented in the chart of the E-mini S&P 500 Futures contract shown below:

More Conservative Playing the Bands

Rather than buying or selling exactly when the price hits the Bollinger Band, the more aggressive approach, a trader could wait and see if the price moves above or below the Bollinger Band and when the price closes back inside the Bollinger Band, then the trigger to buy or sell short occurs. This helps to reduce losses when prices breakout of the Bollinger Bands for a while. However, many profitable opportunities would be lost. To illustrate, the chart of the E-mini S&P 500 Future above shows many missed opportunities. However, in the chart on the next page, the more conservative approach would have prevented many painful losses.

Also, some traders exit their long or short entries when price touches the 20-day moving average. This was the methodology used for going long in the book Trade Like a Hedge Fund.

A different, and quite polar opposite way to use Bollinger Bands is described on the next page, Playing Bollinger Band Breakouts.

Bollinger Bands

Bollinger Bands is a versatile tool combining moving averages and standard
deviations and is one of the most popular technical analysis tools available for
traders. There are three components to the Bollinger Band indicator:

1. Moving Average: By default, a 20-period simple moving average is used. Upper Band: The upper band is usually 2 standard deviations (calculated from 20-periods of closing data) above the moving average.
2. Lower Band: The lower band is usually 2 standard deviations below the moving average.

Bollinger Bands (in blue) are shown below in the chart of the E-mini S&P 500 Futures contract:

There are three main methodologies for using Bollinger Bands, discussed in the following sections:

1. Playing the Bands
2. Bollinger Band Breakouts
3. Option Volatility Strategies
   

Option Volatility Strategies

There are two basic ways to trade volatility:

1. Buy options with low volatility in hopes that volatility will increase and
   then sell back those options at a higher price.
2. Sell options with high volatility in hopes that volatility will decrease
   and then buy back those same options at a cheaper price.

Since Bollinger Bands adapt to volatility, Bollinger Bands give options traders a good idea of when options are relatively expensive (high volatility) or when options are relatively cheap (low volatility). The chart below of Wal-Mart stock illustrates how Bollinger Bands can be used to trade volatility:

Buy Options when Volatility is Low

When options are relatively cheap, such as in the center of the chart above of Wal-Mart when the Bollinger Bands significantly contracted, buying options, such as a straddle or strangle, might be a good options strategy.

The reasoning is that after sharp moves, prices tend to stay in a trading range to rest. After prices have rested, such as periods when the Bollinger Bands are extremely close together, then prices usually will begin to move once again. Therefore, buying options when Bollinger Bands are tight together, might be a smart options strategy.

Sell Options when Volatility is High

At times when options are relatively expensive, such as in the far right and far left of the chart above of Wal-Mart when the Bollinger Bands were significantly expanded, selling options in the form of a straddle, strangle, or
iron condor, might be a good options strategy to use.

The logic is that after prices have risen or fallen significantly, such as periods when the Bollinger Bands are extremely far apart, then prices usually will begin to consolidate and become less volatile. Hence, selling options when Bollinger Bands are far apart, potentially could be a smart options volatility strategy. This strategy is further outlined in The Volatility Course by George A. Fontanills.

Theoretical Option Pricing Models

Binomial Option Pricing and theBlack-Scholes Formula

Although several factors have been considered in what determines an option's worth, it is intuitively obvious that what actually determines the worth of an option is the probability that the option will be in the money by expiration, and by how much. Everything else can be subsumed under these 2 variables.
If a given variable increases the option premium, it is because it increases 1 or both factors. Thus, the reason why a greater amount of time until expiration or a greater volatility increases premiums is because there is a greater chance that the option will be in the money by expiration, and by a larger amount; likewise, premiums are low for an option way out of the money, because there is little chance that the underlying asset will reach the strike price by expiration.

While prices and time intervals are easy enough to measure, what cannot be known with certainty is the volatility of the underlying asset, and therefore, the probability that an option will be in the money or by how much, before
expiration. Historical volatility is not necessarily a good indicator of future volatility, although it does provide some measure of volatility.

Various pricing models have been developed in an attempt to more accurately gauge the true worth of options, or to price them better initially, when they are first created.

The binomial option pricing model starts by evaluating what a call premium should be if the underlying asset can only be 1 of 2 prices by expiration. A variable that can only be 1 of 2 values is known as a binomial
random variable. By subdividing the time into smaller time intervals with 2 possible prices that are closer together, a more accurate option premium can be calculated. As the number of time periods increases, the distribution of possible stock prices approaches a normal distribution—the familiar bell
curve.

The probability of a stock price is proportionate to the height of the curve.

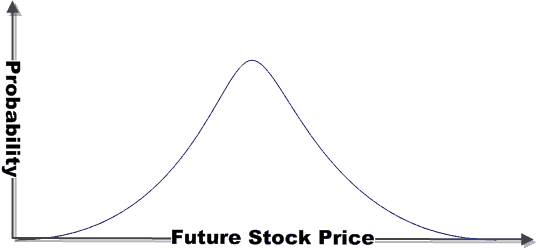The probability of a stock price is proportionate to the height of the curve.
---------------------------------------------------------------------------------
The Black-Scholes formula is the most widely used formula to calculate option premiums. Much easier to use than the binomial option pricing model, it, nonetheless, is dependent on assessing the volatility of the underlying asset, which is denoted by the standard deviation, σ, of the underlying asset prices about the current price.

Although the Black-Scholes formula calculates the premium for a call, the put premium can be calculated by using the put-call parity formula.
Note from this formula, that the standard deviation, σ, which is a measure of volatility, can be calculated if the other variables are known. This is called the implied volatility, because it is implied by the other variables. Some traders compare the implied volatility with the observed volatility to judge whether an option is fairly priced.

Why Volatility Increases Time Value and Option Premiums

Volatility is the unknown change in price of the underlying security over time, and is what gives options any value at all. For instance, consider a hypothetical stock with a price that never changes. An option based on such a stock would never have any time value, because the underlying is always the same price, therefore, no one would want the option—neither put nor call—if it was out of the money. On the other hand, no one would sell an option based on this stock that was in the money, because it would certainly be exercised. Now consider another hypothetical scenario where the stock changed price according to some formula, so that anyone could calculate the stock price with certainty at any time. Again, there would be no time value to any option based on this stock, because its price at any time can be known by anyone. For instance, if this stock were $50 today, and it was known for certain that, before a specific expiration date, it would be $60, then no one would write a call with a $50 strike, unless they were getting $10 per share (although maybe they would charge a little less to get the money sooner) and no one would buy this call unless it were discounted enough to at least equal prevailing interest rates. Thus, it is the unknown fluctuation in the underlying prices that gives options value.
Now consider 2 hypothetical stocks, currently at $50 per share. Stock SSS is relatively stable, and has ranged between $40 and $60 per share over the past year, whereas stock VVV is more volatile, and has ranged from $30 to $70. Further, assume that the chance is 1/5 that either stock will be at some specific price within its historical range, listed in the table, at expiration. Obviously, a call for VVV with a strike of $50 is going to command a higher premium than the same call for stock SSS for the same expiration date, because there is a 20% chance that the VVV call premium will be worth $20 per share, and a 40% chance that it will be worth at least $10 per share, the most that the call for SSS will be worth. It is true that there is a chance that VVV will be at $30 per share, and that SSS will be no less than $40 per share, but this doesn't matter, because if the stock price is less than or equal to the strike price, then the options will expire worthless, and the chance that they will expire worthless is 50% for both stocks. Thus, if the VVV call has a chance of paying $20 per share, but the most that the SSS call will pay is $10 per share, and the chance that they will expire worthless is the same, then it makes sense that the VVV call is going command a higher premium, because it has a greater potential payoff.

Today is Volatile market